viernes, 3 de febrero del 2017
Intervalo de Confianza para la Media Poblacional con Muestras Grandes
Cuando se estima un parámetro, es necesario determinar qué tan cerca está la estimación puntual del valor real.
• Una forma de determinar determinar la precisión de la estimación es con el error estándar
• Otra forma de estimar la precisión es con los intervalos de confianza
• Otra forma de estimar la precisión es con los intervalos de confianza
Se necesita:
α: nivel de significancia
(1-α): intervalo de confianza
Ejemplos:
1. La media y desviación estándar muestrales para todos los pesos de llenado de las 100 cajas, son “µ”= 12.05 y “s”= 0.1. Encuentre un intervalo de confianza de 85% para la media de los pesos de llenado de las cajas.
Distribución de Muestreo de la Proporción
La proporción poblacional se define como la razón entre el número de unidades poblacionales que poseen cierta característica y el total de unidades de la población.Suponga que se tiene una muestra aleatoria X1, X2,….., Xn proveniente de una población que sigue una distribución Bernoulli, Be (p).
Definimos:
donde Xi = 1 con probabilidad p
Xi = 0 con probabilidad 1-p=q
entonces Y cuenta el número de éxitos en n intervalos.
La proporción de “éxitos” en la muestra.
La v.a Y∼ Bi(n,p), por lo que:
µ=np σ2 = npq
y se cumple:
Ejemplo:
En un proceso de Poisson el 20% de los productos tiene algún defecto. Se selecciona una muestra de 100 unidades y se cuenta el número de artículos defectuosos. Determinar la probabilidad de que la proporción de defectuosos se encuentre entre el 15% y 29%.
X: Artículos Defectuosos
Intervalo de Confianza para la Proporción
Conceptos básicos:
Método tradicional:
Es ampliamente usado pero no recomendado.Sea p̂ la proporción de éxitos en un gran número n de ensayos de Bernoulli independientes con probabilidad de éxito p. Entonces el intervalo de confianza tradicional de nivel 100(1-α)% para p es:
Ejemplos:
1. Se hizo una encuesta a 325 personas mayores de 16 años y se encontró que 120 iban al teatro regularmente . Halla con un nivel de confianza del 94 % un intervalo para estudiar la proporción de los ciudadanos que van al teatro regularmente. 2. Tomada al azar una muestra de 500 personas de una determinada comunidad , se encontró que 300 leían la prensa regularmente . Halla con una confianza del 90 % , un intervalo para estimar la proporción de lectores entre las personas de la comunidad.
1. Se hizo una encuesta a 325 personas mayores de 16 años y se encontró que 120 iban al teatro regularmente . Halla con un nivel de confianza del 94 % un intervalo para estudiar la proporción de los ciudadanos que van al teatro regularmente. 2. Tomada al azar una muestra de 500 personas de una determinada comunidad , se encontró que 300 leían la prensa regularmente . Halla con una confianza del 90 % , un intervalo para estimar la proporción de lectores entre las personas de la comunidad.
martes, 07 de Febrero del 2017
Intervalos de confianza para muestras pequeñas
(n < 30)
Cuando tratamos con muestras pequeñas, no podemos invocar el teorema del límite central. Por lo tanto, no podemos utilizar la fórmula para los intervalos de confianza a menos que sean muestras desde una variable aleatoria normalmente distribuida.
Sin embargo, hay una cuestión más: Si conocemos la desviación estándar poblacional σ, entonces todo está bien, y podemos seguir adelante y utilizar la fórmula anterior para el intervalo de confianza para muestras pequeñas (suponiendo que estamos tomando muestras de una variable distribuida normalmente). Pero si, como suele ser el caso, no sabemos σ, entonces si seguimos adelante y utilizamos en su lugar la desviación estándar muestral s, es probable que obtengamos intervalos de confianza que son demasiado pequeños. La razón es que, mientras que la distribución muestral de (x − μ)/σ,
es normal (siempre que x es normal) la distribución muestral de
(x − μ)/s no es normal (a menos que se trate de muestras grandes, en cuyo caso es aproximadamente normal).
Este número de desviaciones estándar es
(x − μ)/σ. Entonces establecemos que equivale a valor −z deseado y resolverlo para x para obtener el intervalo de confianza (después de dividir la desviación estándar por √ n ). Cuando utilizamos s en vez de σ, no podemos utilizar un valor−z, ya que la distribución de (x − μ)/s no es normal, pero se distribuye de acuerdo con la "distribución−t
para diferentes tamaños muéstrales, y utilizamos el valor de tα/2 correspondiente a " n − 1
grados de libertad", que podemos obtener de una tabla
Ley de distribución chi cuadrado
sean X1,X2,X3,....... Xn variables aleatorias independientes que siguen una distribución normal estándar, la variable aleatoria definida por

La esperanza esta dada de la siguiente manera:
viernes, 10 de febrero del 2017
En este día el compañero que expuso acerca de la distribución X2 terminó de exponer su último ejercico dando paso a que la ingeniera de la clase acerca de los Intervalos de confianza para la varianza poblacional.


En este día el compañero que expuso acerca de la distribución X2 terminó de exponer su último ejercico dando paso a que la ingeniera de la clase acerca de los Intervalos de confianza para la varianza poblacional.
Intervalos de Confianza para la Varianza Poblacional
Supóngase que se requiere estimar la varianza y se dispone de una muestra x1,x2,...,xn que suponemos proviene de una ley normal.
Un intervalo de confianza viene dado por:
Posterior a esto la ingeniera realizó varios ejercicios en clase para que los temas explicados queden más claros y aplicar la teoria vista anteriormente.
Luego de las explicaciones de la ingeniera, el siguiente grupo expuso acerca de las Pruebas de Hipotesis.
Pruebas de Hipótesis para la media poblacional con muestras grandes
Definicion:
Prueba de hipótesis es una prueba estadística regida por tablas donde encontramos los valores que disocian un resultado típico o de alta probabilidad de un resultado atípico.
Nos permite determinar si la hipótesis es un enunciado razonable y no debe rechazarse o si no es razonable y debe ser rechazado.
Hipótesis nula H0: afirmación acerca del valor de un parámetro poblacional.
Hipótesis alterna H1: afirmación que se aceptará si los datos muestrales proporcionan evidencia de que la hipótesis nula es falsa.
Nivel de significancia: Es la máxima cantidad de rechazo que estamos dispuestos a aceptar. (α = 0.05 o en su forma 5%)
Valor crítico: el punto que divide la región de aceptación y la región de rechazo de la hipótesis nula.
P-valor: Es la probabilidad, bajo el supuesto que H0 es verdadera.
Pruebas de Hipótesis para la media poblacional con muestras grandes
Sean:
n: tamaño de la muestra
µ0: media poblacional
: media muestral ------> µ
σ: desviación estándar poblacional
s: desviación estándar muestral
Propiedades:
1.-Trata de un trabajo de investigación en el que se plantea dos hipótesis mutuamente excluyentes
2.-Al aumentar el tamaño muestral las pobabilidades de rechazo y aceptación decrecen a la vez.
3.-Se dispone de una muestra de una población determinada
4.-Muestra grande (n > 30)
5.-Entre menor sea el P-valor, se puede tener más certeza de que H0 es falsa.
6.-Entre mayor sea el P-valor, es más factible H0, pero nunca se puede tener la certeza de que H0 sea verdadera.
7.-Una regla general indica rechazar H0 cada vez que P 0.05. Aunque esta regla es conveniente, no tiene ninguna base científica.
Para probar una hipótesis nula de la forma H0: µ ≤ µ0, H0: µ ≥ µ0, o H0: µ = µ0:
Calcule el puntaje z (estadístico de prueba):
Si σ es desconocida se puede aproximar con s.
Calcule el P-valor. Éste constituye un área bajo la curva normal, que depende de la hipótesis alternativa de la siguiente manera:
Hipótesis alternativa P-valor
H1: µ > µ0 Área a la derecha de z
H1: µ < µ0 Área a la izquierda de z
H1: µ ≠ µ0 Suma de áreas en las colas correspondientes a z y -z
Regiones de rechazo y aceptación de la hipótesis nula (H0)
Pasos para la realización de una prueba de hipótesis
1.-Defina H0 y H1.
2.-Suponga que H0 es verdadera.
3.-Calcular un estadístico de prueba. Éste constituye un estadístico que se usa para evaluar la fuerza de la evidencia en contra de H0.
4.-Calcule el P-valor del estadístico de prueba. El P-valor es la probabilidad, suponiendo que H0 es verdadera, de que el estadístico de prueba tenga un valor cuya diferencia con H0 sea tan grande o mayor que el realmente observado. El P-valor también se llama nivel de significancia observado.
Despúes de las respectivas indicaciones y acabando de dar toda la teoría los compañeros procedieron a realizar ejercicios, para que así los temas explicados en la clase queden más claros.








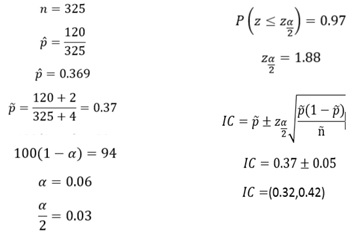






No hay comentarios:
Publicar un comentario